Neural Networks At It's Core.
Exploring the Mathematical Foundations and Practical Implementations of Neural Networks and the algorithm associated with it.
Introduction
Hello readers! 🌟 Welcome to the thrilling world of AI and ML! Whether you're an aspiring AI professional ready to kickstart your career or a tech enthusiast passionate about uncovering the secrets behind cutting-edge technology, this blog is your perfect entry point. Join me as we delve deep into neural networks, exploring their mathematical foundations like cost functions and activation functions. I'll guide you through the basics step-by-step, although a general understanding of linear algebra is a must! Get ready to unlock the secrets of how machines learn, understand the magic behind AI predictions, and empower yourself with knowledge that is shaping the future.
What Is Neural Network?
Let's ditch the technical definitions you can easily find online. Instead, I'll explain neural networks in simple terms, using illustrations and just the right amount of math.
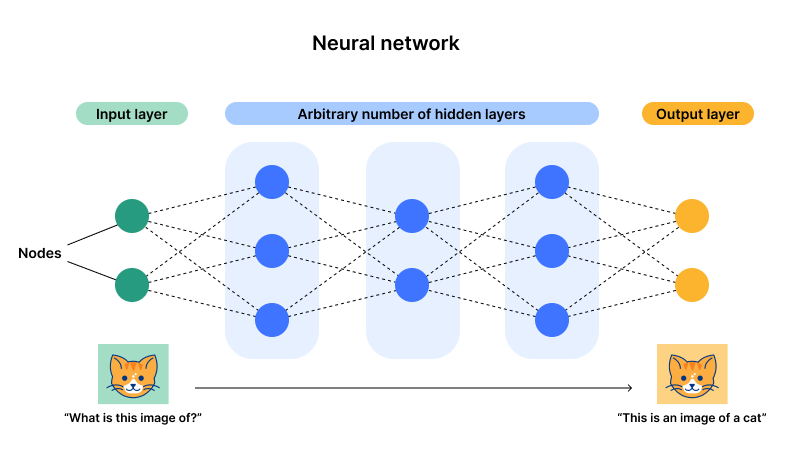
Neural networks are composed of a series of layers:
Input Layer: This is where the input data enters the network.
Hidden Layers: These are the intermediate layers where all the magic happens—data is processed, and patterns are detected.
Output Layer: This is where the network produces the final result.
The illustration above clarifies this structure. A neural network can have multiple layers and neurons, making it highly flexible and capable of handling complex tasks.
The concept of Neural Networks draws inspiration from the intricate functionality of the human brain. In our brains, billions of neurons are interconnected through nerve cells, enabling the processing and transmission of chemical and electrical signals. Similarly, artificial neural networks mimic this biological structure to process information, using mathematical functions to compute and pass data from one neuron to another.
To understand how data flows within an artificial neural network and the role of each neuron (or node), therefore we must delve into the foundational concept of the perceptron.
Perceptron
A perceptron is the simplest type of neural network. To put it simply, a single layer network is known as a perceptron, whereas multiple perceptron or multiple layered networks form what we call Neural Networks. Essentially, a perceptron is a single unit of a Neural Network.

Perceptron Learning Rule
In order to understand how multiple layers are interconnected and work together in a neural network, it's crucial to grasp the functioning of a perceptron, which represents a single layer.
A perceptron takes multiple inputs (𝑥ₙ), each associated with a specific weight (wₙ), and incorporates a bias term to adjust the activation function either up or down. Hold on with me—you might be wondering what terms like weight, bias, and activation function mean. Don't worry, we'll dive into those concepts shortly!
Perceptron Algorithm
Calculate Weighted Sum of Inputs (Including the Bias)
Each input (𝑥ₙ) is multiplied by its corresponding weight (wₙ).
A bias term is added to the weighted sum to shift the activation function up or down.
Compare Weighted Sum to Threshold Value
The weighted sum is compared to a predefined threshold value.
This comparison determines the binary output using a binary classifier.
Binary Classifier
A binary classifier is a supervised learning algorithm where the model categorizes data into one or more parts rather than giving us the numerical value it gives us alphanumerical value. In our case, it will categorize the output as either 0 or 1, based on whether the weighted sum exceeds the threshold value.
Next, let's delve into the mathematical foundation that powers this process.

The output generated by a perceptron is based on the input values 𝑥₁, 𝑥₂, 𝑥₃......𝑥ₙ. The output can only have two values (binary classification), usually 1 or 0.
The summation function (represented by Σ) multiplies the inputs with the weights plus the bias term and then adds them up. This can be represented using the following equation:
y = 𝑥₁*w₁ + 𝑥₂*w₂ + 𝑥₃*w₃ + ..... 𝑥ₙ*wₙ + b
Let's break down each term.
Terminologies
Weights: Weights represent the strength of the connection between two neurons. They indicate how much impact the output of one neuron will have on the input of the next neuron in case of neural network where output of neuron is an input to the next neuron. Weights can be any real number from negative infinity (∞) to positive infinity (∞).
- Mathematically: output = Σ(weight * input) + bias
Bias: Bias in a neural network adjusts the weighted sum of inputs before applying the activation function to a neuron. This adjustment shifts the neuron's activation threshold, enhancing its ability to fit data and model complex patterns. Without bias, the neuron's decision boundary—where it separates different classes—must pass through the origin, limiting its flexibility in complex scenarios. This constraint reduces the network's capacity to learn diverse functions, as it's constrained to functions passing through the origin in input-output space and it result in introducing the linearity in the neural network
Mathematically, without bias, the output is calculated as:
output= activation function ( 𝑥₁*w₁ + 𝑥₂*w₂ + 𝑥₃*w₃ + ..... 𝑥ₙ*wₙ )
This formulation mandates that if all inputs 𝑥₁ + 𝑥₂ + 𝑥₃ + ..... 𝑥ₙ are zero, the output must also be zero (or a fixed value). This severely restricts the types of functions the neural network can represent.
Introducing bias modifies the formula to:
output = activation function (𝑥₁*w₁ + 𝑥₂*w₂ + 𝑥₃*w₃ + ..... 𝑥ₙ*wₙ + b)
Here, bias allows the neuron's activation function to operate independently of the inputs, enabling the network to learn and model a broader range of functions, thereby enhancing its capability to solve complex problems.

You might be wondering about what's the purpose of assigning a bias value when the input is already zero. Doesn't it make like we are giving a fake value then?
Well to justify that consider a scenario where the absence of input features is meaningful. For example, in a recommendation system, a user not watching a particular genre of movies might be informative. Without bias, the neuron wouldn't activate at all with zero input. Bias allows neurons to have a baseline level of activation, even with no input, capturing these "absence" signals.
Activation Function: The summation is passed through an activation function, the activation function converts the output to certain range so that we could identify that whether neuron is activated or not as I discussed above weight can be ranged from negative infinity (∞) to positive infinity (∞) so without any particular range it will be hard to determine the activation of the neuron will occur or not. The summation is passed through an activation function. The activation function does some type of operation to transform the sum to a number that is often times between some lower limit and some upper limit. This transformation is often a non-linear transformation. We use binary classification to distinguish whether it will activate or not.
The result of the weighted sum can be any number, but for neural networks, we want the activation values to be within a specific range to determine if the neuron will fire or not. Therefore, we use an activation function to squish the real number line into a specific range. Let's look at how activation functions work, there are many activation out there however for sake of an understanding will take sigmoid activation function.
Sigmoid Activation Function
The sigmoid function takes an input and performs the following transformations
For very negative inputs, the sigmoid function will transform the input to a number very close to 0.
For very positive inputs, the sigmoid function will transform the input to a number very close to 1.
For inputs close to 0, the sigmoid function will transform the input into a number between 0 and 1.

Here's how it looks mathematically:
Where σ is the sigmoid function. This function ensures that the output is always between 0 and 1, which helps in determining the activation of a neuron.

And that's just one neuron! Mind-blowing, right? Similarly, every other neuron in the layer has its own set of weights connected to neurons in the subsequent layer, each with its own bias. These biases are added to the weighted sum before being squished through a sigmoid or any other activation function. This interconnected structure allows neural networks to learn and model complex patterns in data. And all of this is just the connection from the first layer to the second and Imagine this process repeating endlessly, layer after layer—that's what makes it a neural network! And yes, at its core, a neural network is essentially just a lot of sophisticated math!
More Neurons
Wait this isn't the end, what if a calculation goes wrong and needs to be recomputed? Or in another scenario, what if a neuron needs tweaking? The real question isn't just how it's done, but rather how the computer knows which neuron to adjust. This is where tracking comes into play—it's essential for keeping tabs on each neuron's role and performance within the network.

However, using the sequential approach to compute each neuron individually becomes impractical in real-world scenarios with thousands or millions of layers and billions of neurons. This method would require extensive computational effort and significantly slow down the network's performance. Instead, we must employ matrix-vector multiplication to compute the activations of all neurons in the next layer simultaneously.
This approach optimizes efficiency by leveraging parallel processing capabilities, thereby enhancing the overall speed and effectiveness of the neural network.
- Starting by organizing all the activation from first layer into a vector.

- W is a column vector containing the weights for the subsequent layer.

Now instead of taking bias for each neuron explicitly will make a additional vector for bias and adding with the previous vector.

And lastly will keep the activation function outside so that it will apply to the every neuron.

It totally make sense, if you have a good understanding of matrices you know how easy it gets for calculation, matrix have various implementation in real life it's not only limited to computer science but in various fields like meteorology for weather forecasting, electrical circuits, the programmers use matrix for encrypting the message and in fact the display where you are reading this blog the matrix helps in rendering pixels in your screen.
Define Neural Network
Neural Network is a just a function which mimics the behavior of a human brain and like human brain it has neurons that holds the number, and the number it holds depends on the input you feed in, in fact it will be more appropriate to say that neuron is a function. It takes the activations from all the previous layers and fires out a number within a specific range, usually between 0 and 1, depending on the activation function used. This process involves iterating through an entire matrix-vector product with a sigmoid or other activation function. Actually speaking the entire network is a function! Absolutely pathetic function which goes through millions and billions of neurons and it does millions and billions time the same calculation.
Conclusion
We've journeyed from understanding the workings of a single neuron to how multiple neurons pass data between layers, exploring their operations and mathematical foundations. Now some people might have lots of questions that needed to answer such as How do weights get their values? How is the bias value determined? And what happens if a calculation goes wrong and needs tweaking? While I mentioned the need for precise notation, but I didn't delve into how recalculations occurs i.e. how the correction of calculation done. Your concerns are valid! however these aspects involve their own algorithms and explicit implementations, making it difficult to cover everything in a single blog. I am not a regular writer however if god wills, I will definitely write about them as well.
